Proyección ortogonal
De Wikipedia, la enciclopedia libre
En geometría Euclidiana, Proyección ortogonal es aquella cuyas rectas proyectantes auxiliares son perpendiculares al plano de proyección (o a la recta de proyección), estableciéndose una relación entre todos los puntos del elemento proyectante con los proyectados.
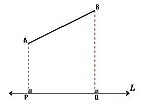
En el plano, la proyección ortogonal es aquella cuyas líneas proyectantes auxiliares son perpendiculares a la recta de proyección L.
Así, dado un segmento AB, bastará proyectar los puntos "extremos" del segmento –mediante líneas proyectantes auxiliares perpendiculares a L–, para determinar la proyección sobre la recta L.
Una aplicación de proyecciones ortogonales son los teoremas de las Relaciones métricas en el triángulo mediante las cuales se puede calcular la dimensión de los lados de un triángulo.
El concepto de proyección ortogonal se generaliza a espacios euclidianos de dimensión arbitraria, inclusive de dimensión infinita. Esta generalización juega un papel importante en muchas ramas de matemática y física.
En el plano, la proyección ortogonal es aquella cuyas líneas proyectantes auxiliares son perpendiculares a la recta de proyección L.
Así, dado un segmento AB, bastará proyectar los puntos "extremos" del segmento –mediante líneas proyectantes auxiliares perpendiculares a L–, para determinar la proyección sobre la recta L.
Una aplicación de proyecciones ortogonales son los teoremas de las Relaciones métricas en el triángulo mediante las cuales se puede calcular la dimensión de los lados de un triángulo.
El concepto de proyección ortogonal se generaliza a espacios euclidianos de dimensión arbitraria, inclusive de dimensión infinita. Esta generalización juega un papel importante en muchas ramas de matemática y física.
[editar] Casos de proyección ortogonal en el plano
- Proyección ortogonal de un punto
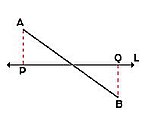
- La proyección ortogonal de un punto P en una recta L es otro punto A que se obtiene trazando una línea auxiliar perpendicular a L desde el punto A. Lógicamente, si el punto P pertenece a la recta L, coinciden: P = A .
- Proyección ortogonal de un segmento
- Caso general: si el segmento dado AB no es paralelo la recta L, la proyección ortogonal es segmento PQ que se obtiene trazando líneas perpendiculares a L desde los puntos extremos. La magnitud de la proyección siempre es menor que la del segmento dado.
- Si el segmento PQ y la recta L son paralelos, la proyección será: AB = PQ, que se obtiene de forma análoga.
- Si el segmento AB tiene un punto común con la recta L, la proyección se obtiene de modo similar.
- Si el segmento AB corta a la recta L, la proyección se obtiene de forma análoga.
Relaciones métricas en el triángulo
De Wikipedia, la enciclopedia libreLas relaciones métricas en el triángulo son cinco teoremas o propiedades, incluyendo la ecuación del Teorema de Pitágoras. Estas son válidas, exclusivamente, en el triángulo rectángulo y se aplican sobre las dimensiones de los catetos, hipotenusa, la altura relativa a la hipotenusa y los segmentos determinados sobre ésta como proyecciones de los catetos de triángulo.Contenido
[ocultar][editar] Relaciones métricas en el triángulo rectángulo
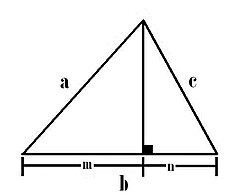
Dado un triángulo rectángulo ABC (véase la imagen), con ángulo recto en C, donde:- c es la hipotenusa,
- h es la altura relativa a la hipotenusa,
- p y q son los segmentos determinados en la hipotenusa,
- El cuadrado de un cateto es igual al producto de la hipotenusa por la proyección ortogonal de este mismo cateto sobre la hipotenusa:
- comprobación
- El cuadrado de la medida de la altura es igual al producto de las proyecciones ortogonales de los catetos sobre la hipotenusa:
- comprobación
- El cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos (Teorema de Pitágoras).
- comprobación
- El producto de los catetos es igual al producto de la hipotenusa por su altura:
- comprobación
1) a partir de las superficies o áreas:
- El inverso del cuadrado de la altura de la hipotenusa es igual a la suma de los inversos de los cuadrados de los catetos:
- comprobación
 :
:
[editar] Relaciones métricas en el triángulo oblicuángulo
Euclides vio un inconveniente: en un triángulo rectángulo c2 = a2 + b2 ¿cuanto debería valer numéricamente el lado a en un triángulo oblicuángulo? Euclides despejó su duda con la primera ley de Euclides para los triángulos oblicuángulos.
[editar] Primer teorema de de Euclides
El cuadrado de uno de los lados de un triángulo oblicuángulo es igual a la suma de los cuadrados de los otros dos lados menos el doble del lado relativo a la altura por la proyección del lado opuesto al que se quiere hallar.
Euclides notó que aunque no se generen triángulos semejantes al trazar la altura se generan dos triángulos rectángulos en los cuales se puede aplicar el teorema de Pitágoras:
empezamos en el triángulo de la izquierda
[editar] Segundo teorema de Euclides
En un triángulo obtusángulo, el lado opuesto al ángulo agudo al cuadrado es igual a la suma de los cuadrados de los catetos más el doble de la base por la proyección de la altura trazada desde uno de los ángulos menores.
Euclides notó que al trazar la altura exterior se generan dos triángulos rectángulos (AHC y BCH)
en el más pequeño (AHC)
[editar] Cálculo de las líneas notables de un triángulo
A partir de los dos teoremas anteriores se deriva fórmulas para el cálculo de las líneas notables de un triángulo. A continuación vamos a ver estos 5 teoremas con su comprobación.
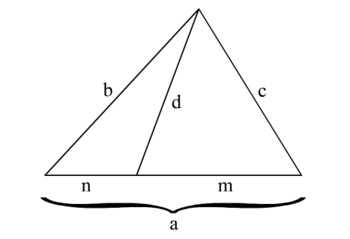
[editar] Teorema de Stewart (cálculo de la ceviana)
Stewart dice que el producto resultante entre una ceviana de un triángulo al cuadrado y de la base de este es igual a la al cuadrado por la proyección del cateto opuesto más la suma del segundo cateto al cuadrado por la proyección del cateto opuesto a este menos el producto resultante entre las multiplicación de las proyecciones de los catetos y la base.
Su formulación matemática es:
Donde b y c son los lados "laterales" respecto a la ceviana d correspondiente al lado a, n y m los segmentos de la base designados por la misma ceviana.
[editar] Teorema de la mediana
En geometría, el teorema de Apolonio, también llamado teorema de la mediana, es un teorema que relaciona la longitud de la mediana de un triángulo con las longitudes de sus lados.
Para cualquier triángulo ΔABC (véase fig. m1), si M es la mediana correspondiente al lado c, donde AP = PB = ½ c, entonces :Teorema de Apolonio (teorema de la mediana)
Para todo triángulo la suma de los cuadrados de dos lados cualesquiera, es igual al la mitad del cuadrado del tercer lado más el doble del cuadrado de su mediana correspondiente.
Del teorema de Apolonio, también llamado "teorema de la mediana", pueden deducirse varias fórmulas prácticas (válidas para cualquier triángulo), éstas permiten calcular a partir del conocimiento de tres elementos, a un cuarto elemento desconocido, (los elementos en cuestión son lados y medianas). La siguiente tabla muestra un resumen de las mismas (con notación acorde a la figura de la propia tabla) :
Triángulos — Medianas ( fórmulas prácticas II ) 
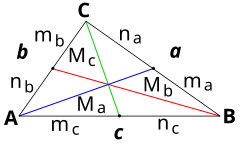







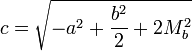



( Lados: a, b y c ) — ( Medianas: Ma, Mb y Mc )[1] — ( Semilados: ma=na = ½ a , mb=nb = ½ b y mc=nc = ½ c ).
Caso particular :
En un triángulo rectángulo isósceles la mediana relativa a la hipotenusa es igual a la mitad de esta, (véase Corolario 1 del teorema segundo de Tales), asumiremos para la ecuación siguiente que dicha hipotenusa se denomina c).
Donde M es la mediana correspondiente a la hipotenusa denominada c.
[editar] Teorema de la bisectriz interior
Teorema de la bisectriz interior
La bisectriz interior de un triángulo al cuadrado es igual al producto de los lados menos el producto de los segmentos de la base determinados por la bisectriz.
Donde:
X:Bisectriz interior
comprobación
por el teorema de semejanza en la bisectriz interior

despejando

por el teorema de Stewart:

reemplazando an por cn

despejando

[editar] Teorema de la bisectriz exterior
La bisectriz exterior de un triángulo al cuadrado es igual al producto de los segmentos deteriminados por la bisectriz menos el producto de los lados.
Archivo:Teorema de la bisectriz exterior.jpg

Donde:
X:Bisectriz exterior:
comprobación
Recordando el teorema de semejanza en la bisectriz interior

despejando

Luego, ejecutando el teorema de Stewart:

reemplazando an por cn:

luego

despejando expulsa que:

[editar] Teorema de la altura
También conocido como el teorema de Herón. La altura de un triángulo es igual a:
Aplicando el primer teorema de Euclides:

Aplicando el teorema de Pitágoras en el triángulo BHC:

Aplicando diferencia de cuadrados

transformando HC

Sumando:

ejecutando el binomio al cuadrado:

ejecutando la diferencia de cuadrados y transponiendo el (2b)2

para a+b+c = 2p

despejando la altura expulsa que

[editar] Teoremas auxiliares en los cuadriláteros
[editar] Teorema de Ptolomeo
En todo cuadrilátero inscriptible el producto de las diagonales es igual a la suma de los productos de los lados opuestos del cuadrilátero

Donde:
D1,D2: Diagonales del cuadrilátero
a, b, c, d : Lados del cuadrilátero
[editar] Teorema de Viette
En todo cuadrilátero inscrito la relación de las diagonales es igual a la relación entre la suma de los productos de las longitud de sus lados que forman a los extremos de las diagonales.

Donde:
D1,D2: Diagonales del cuadrilátero
a, b, c, d : Lados del cuadrilátero
[editar] Teorema de Euler
En todo cuadrilátero la suma de los cuadrados de los lados es igual a la suma de los cuadrados de las diagonales adicionado con el cuádruple del segmento de une los puntos medios de las diagonales

Donde:
D1,D2: Diagonales del cuadrilátero
a, b, c, d: Lados del cuadrilátero
X: Segmento que une los puntos medios de las diagonales




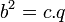
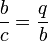
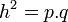



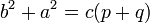































 ).
).

Muy Bueno!!!
ResponderEliminarSe puede aplicar la geometría a los fenómenos físicos Naturales de la Tierra.
ResponderEliminarhola gustavo, claro que si
ResponderEliminarMuy Bueno,espero te guste el mio.
ResponderEliminarQue buen compendio de geometría, me hace recordar los tiempos de geometría analítica en la catolica...
ResponderEliminar:'v geometria Euclidiada de Jose Rodolfo Londoño Hahahaha.
ResponderEliminarFuentes??
ResponderEliminar